Note: This is an updated version of the music theory beginners' guide.
Please use the table of content to check the guide overview
- Advantages of Learning Music Theory
- Sharp and flats
- Semitone and Wholetone
- My Approach To Learning Major and Minor Scale (Easy Way)
- Music Interval Simplified
- Minor Intervals
Note: The goal of this guide is to help aspiring music producers finding it difficult to understand the basic aspect of music theory. If you are a pianist who is aiming to learn how to play the piano, I am sorry this guide is not for you (Go find a piano tutor), but if you are finding it difficult using music theory in the Daw, then this guide is worth checking out. 😊
Advantages of Learning Music Theory
Music Theory helps to understand what music does, and it also helps to understand the structural arrangement of the composition of music, that is it helps to perceive the arrangement of how music is composed.
More straightforwardly, it is a means of understanding the language of music.
Music Theory follows specific rules that help in the composition of music, but sometimes you break the rules, and it turns out to be your ah-ah moment, you ask yourself:
"Why does this sound great?"
This is a tough question for those that don't have an idea about the fundamental rule.
You break the rules when you know the primary standards, in that sense, it helps to deepen our knowledge of how we see the practical aspect and also helps in improving our composition skills.
Making music is a fundamental thing, and you generally don't need to take music theory classes to be able to compose a piece of good music, but understanding theory helps in a faster approach to how you eliminate what doesn't sound right to you (It's like a short-cut of composing music).
Practically, you can compose music if you don't know the theory behind it, but that would take way longer than you can imagine, how does music help in this sense?
Music theory helps to get there faster and lets you understand what might work and what won't work.
I want you to perceive music theory as arranged cards that are correctly ordered on top of each other, for you to arrange the cards correctly, you must know the principle of why one card should be above or below another card.

Now, let our card denote our musical Note, Note is music sound or tone and is the smallest element of composing a piece of music, in the next section, we would explore sharps and flats, see you in the next section.
Sharp and flats
The Sharp and flats are all about movement and the black key could either be a Sharp or Flat and that depends on how we move and how we decide to name it (at least on a piano).
Sharp
Sharp means to move a note higher and flat means to move a note lower.
Note: I need you to note the word "BE", all this means is that B and E don't have a black key, making sense? would further explain below, use your DAW piano to follow along.
For Example, let's say we are playing a melody, and we are told to move from (C to F), we first move from (C to C#) (which means you have moved a note higher).
Thus we call that C sharp(#) -> we then move from C# to the next note which is D (not a black note, let's proceed) -> from D to the next note would be called D sharp(#) (Again, we are moving higher) ->
moving from D# to the next note is E (no sharp here, remember the word "BE") -> from E to the next note is F (again no sharp. ), movement between two white notes has no sharp.
Flat
What about a Flat? It means moving a note lower, and it is denoted ♭, e.g. B♭(B flat)
For example, let's say we are to move from note C to the lower black key, we call that a movement C to B♭(flat) and not C to A#. Why? Because we are moving lower and not higher.
Why do I have to tell you flat, if it has the same key as sharp (#)?
Like it or not, you are going to encounter flat, and I don't want you to be confused when someone says E♭ (E flat).
Let me give you a trick to help you remember b(flat). When you see the note C#, the next higher note is the name of the flat, which is D, and that gives us(C# or D♭).
More example:
D# or Eb
F# or Gb
A# or Bb
G# or Ab
C# or Db.
Again, remember the movement, if you are moving higher and you encounter a black key, it is sharp, and if moving lower and you encounter a black key it is flat.
Conclusion: The black keys can have two names, either sharps or flats depending on your movement.
Turn on the cc, and set it to English if you want to learn it smoothly
Semitone and Wholetone
Semitones could either be called half steps or halftones and a Whole Tone can also be called Whole Steps.
In this guide, I will refer to them as Semi-Tones and Whole Tone, have in mind that they are called half steps and whole steps as well.
Semitone
Semitones are two keys together with no key between, looking at our piano roll, any two keys or notes that are together is a semitone. e.g. a movement from C to C# or D to D# or E to F are together, and they have no key between them, we refer to that as a semitone.
Example
How many semitones is C to F?
You count all the note up to F, e,g (C to C#) is One (1) semitone, C to D is Two (2) semitones, (C to D#) is Three (3) semitones, (C to E) is Four (4) semitones and (C to F) is Five (5) semitones.
Most people are confused with the counting of semitones; all you need to remember is that a semitone is two notes beside each other with no key in between.
What does that have to tell us?
When you count in semitone, you don't count a single note, you count two notes next to each other, and that gives you a semitone.
When you count in semitone, you don't count a single note; you count two notes next to each other[/caption]
Confusing? use your DAW piano roll to test things out yourself; you can either use your PC/Mac keyboard to play multiple keys at once or click on each key with your mouse.
WholeTone
What is the whole tone?
It is two-key together and a key between, it can either be black or white.
Looking at our piano roll, the movement from (C to D) is a whole tone, why? Because we have a key between the notes, you will always skip a key.
Another way to look at a whole tone is that two (2) semitones make a whole tone, the movement from (C to D) is two (2) semitones; hence it is a whole tone, either way, is a brilliant approach in getting a whole tone.
Example
How do you count five (5) whole tones starting from C?
We can do this in two ways. The first is having it in mind that a whole tone is two keys with a key in between, and the second is two (2) semitones to make a whole tone.
First approach:
A whole tone is two keys with a key in between
(C D E F# G# A#), simple, I just skipped one note, the first note is C, I skipped (C#, D), I skipped D# (remember, two notes, with a note in between).
It looks like this in the Daw, I am using Fl Studio, and I firmly believe every single Daw has a similar appearance.
Now, use the DAW piano roll to experiment with what you just learned:
Alternative Approach (Skip if you understand the above section):
(C to D) is 2 semitone (1 whole tone) -> (D to E) is 2 semitone (1 whole tone) -> (E to F#) is 2 semitone (1 whole tone) -> (F# to G#) is 2 semitone (1 whole tone) -> (G# to A#) is 2 semitone (1 whole tone).
How many whole tones are there? Five (5) whole tones.
So, there are five whole tones between (C and A#).
When someone tells you to move a semitone higher, then you know it's the next tone beside it, and if it is a whole tone, you move two (2) semitones or make sure a key is between two notes.
My Approach To Learning Major and Minor Scale (Easy Way)
A Scale comprises semitones and whole tones, and the majority of scales are seven-note scales.
The scale comes from a Latin word that means "Ladder" The direction you can go on a ladder could either be up or down.
To use a ladder, you foot it in the desired location you intend to use it.
A scale is a fundamental piece in which music is built, and Scales gives you a set of ordered note in which you can create melodies, harmonies, and chords.
Building a Scale
To construct a scale you start from a particular note you intend to build the scale, e.g. Key C, and you could either go in ascending or descending order. (remember the ladder)
You don't necessarily need to start from the first note of the scale; you can start from any note on the scale.
I would show you how to figure out the notes in a scale, keep reading
Instead of playing random notes, scale helps you figure out what notes are to be used in a particular key and what chords to expect, It gives you a quick idea of what to play and what notes go together.
There are lots of scales in western music, but the common ones are major and minor scales, and they both comprise 7 notes.
The next thing I will show you is a trick on how to create a major or minor scale without overthinking.
What I mean is that when you want to work in any key (e,g D# or F, etc.), you would be able to draw out the notes in the scale.
There are two tricks to creating a major and a minor scale, the first one is for major and the second one is for minor, let's deal with the first.
Major Scale
Let's say you are told to play a melody in C major scale, in other for you to play effectively, you should at least, know the notes that comprise the C major scale.
The method I am about to show you is irrelevant to the C major scale, although it works with any notes, as long as it's a Major scale.
C major scale contains all the white notes (C, D, E, F, G, A, B, and C), so that is easy to figure out on your own, we would apply the trick to other notes in the major scale.
All major scales have either sharps or flats; never both (except for C-major which has no sharps or flats.)
What if we want to quickly map out the notes in D Major Scale or any other major scale, how do we do it using the so-called method?
The method involves three simple steps:
First, Assume you have two lines separating each other since we want to draw all the notes we have in D major, we draw the first line on D, and since the lines are separating each other, we skip (D#), and draw the second line on E.
Assume you have two lines separating each other
Second, Assume the two lines separating each other comes together, while still being separated from the previous line we drew.
The last line we drew was E, since it's been separated from the ones coming together, we skip the next note F, and draw two lines together having (F# and G).
Assume the two lines separating each other comes together, while still being separated from the previous line we drew
Third, This is the combination of the first and second methods, but the second step would become a single line instead of 2.
This means we have three lines separating each other.
Draw the three-line each separating one other.
The notes in D major scale are (D - E - F# - G - A - B - C#).
This works for any notes on the Major scale, summarising the method:
- Two lines separating from one another
- The two lines come together while being separated from the previous lines, and lastly
- The combination of the first and second but second steps would become a single line, giving us three lines separating one another.
This method works for any major key as long as you follow the order, to prove to you it works for any key, let's try another example in G#
Minor Scale
What about the minor scale? The minor scale method is more straightforward, and the technique involves using method 2's in between trio 1 (3 isolated notes), I know this sounds weird, but I am going to elaborate.
Using the C minor scale:
Since we are on a C minor scale, we have the first note on C (which serves as the first isolated note), and according to the method, we have 2's in between trio 1, meaning we have two notes together separated by an empty note.
We got our first single note on C, which means we needed two notes to separate the first note, which is (D & E♭).
Our next single note would be F (the second isolated note) and our next two-note would be (G and A♭), and the last isolated note would be B♭ , voila, you just constructed the C minor scale, confusing? It shouldn't be.
Remember I said 2's (two-note next to each other two times) in between trio 1's (three single notes), and that's it.
This can be used to figure out any minor scale you can move it to whatever key you want, and it is still going to be correct.
Let's get to know the musical interval.
Music Interval Simplified
Interval is the distance of one note to another note, and each note has its pitch (how high or low a musical note sounds).
We measure the distance of intervals in semitones; this section is related to semitones and whole tones if you haven't yet read semitones and whole tones parts, I will highly recommend you do that first, and when you are done, come over to this chapter for continuation.
They are different reasons why you should know and understand intervals, for example, instead of saying the distance between notes C and D is two (2) semitones apart, we mean it is a second interval.
Also, Learning the concept and how intervals are used in music is very useful, you need to understand the notes that make up each interval, so that you can identify and select the right note for building harmonies, chords, and melodies in between.
If you follow my explanation in this lesson thoroughly, you would be able to build any type of intervals without much thinking, follow the logic and expect the best.
In our last lesson, we explore a scale, and how to build Major and Minor scales, when working with scale, you need to remember all the notes that make up a particular scale to play effectively.
If you want to play a melody in D major, you select notes in D Major, and if you're going to play in E minor, you pick notes in E minor.
With intervals all you need to remember is the distance, if you remember the distance, then everything stays the same.We are thinking about the relativeness here instead of the absoluteness, don't worry, I will make things clear.
Relative means sharing the same properties, you can see the distance is the same as I am moving around the notes
If you are to play in C Maj, you would typically play or draw the note C first, then build on from there, and if you are to play in G minor, you will most likely find the note G first and build on from there.
I am going back to our C major scale which contains (C, D, E, F, G, A, and B), Instead of telling you to play (C - E - G).
The interval formula would be 1,3,5 that is the formula for the major triad, I know that doesn't make sense now but bear with me, I will clear things up.
Interval is the distance between two notes and they are the building block of any music.
Let's see the different types of intervals we have, and things would become more evident like we have different kinds of scales, We also have different kinds of intervals.
Major Intervals
If you want to build a Major chord (we would talk more about chords in the next part) to harmonize a melody or if you are playing a melody in Major scale, playing major intervals would be the most appropriate one that would work with your tune.
Major 2nd Interval
How do we measure Major Intervals?
Let's say we are in the C major scale (C, D, E, F, G, A, and B) and we play (C - D).
This is the major second interval, if confused, count the number C(1) and D (2) = 2nd Interval and since we are in the Major scale, we refer to that as a Major 2nd Interval
You just played a Major 2nd, how is that a major second?
An interval is a distance in pitch between two notes, to find the intervals between (C and D).
You start the count from the bottom note, which is C(1), and the top note in the scale which is D(2), so the interval between C and D is a major second, and the quality is a Major, remember we are in the major scale.
If you are still baffled by the counting, it's simple, how many notes are there, C(1) and D(2), a Major second.
Note: You are only counting the notes in that scale and not the note outside of the scale.
The beauty of the interval is that the distance always stays the same, no matter what the starting point is. For example, the distance between (C to D) is the same as the distance between (D to E), (F to G), and (A to B), they are all a Major second.
The distance always stays the same
Major 3rd Interval
Let's take more examples: If you play (C and E), then you just played the third interval, C(1), D(2), E(3) and we name it a Major third.
Remember we are in a Major scale, E and G [E(1) F(2) G(3)], D and F [D(1) E(2) F(3)], and so on are also a Major third because they represent the same distance and have the same relationship.
The major third interval
If you are baffled by the counting, it's simple, how many notes are there, C(1), D(2), and E(3) a Major third.
Note: You are only counting the notes in that scale and not the note outside of the scale.
The distance between certain intervals always stays the same no matter where you go on the piano roll, all you need to remember is the bottom note (the first note), the only thing that changes is the note, the number doesn't change.
A simple scenario in the C Major scale. (C, D, E, F, G, A, and B), If you play C and D, this is how it works:
Hey dude, I can see you started from C, so that is 1, and I can see the second note you played is D, which is 2, are we on the major scale? Yes, I will call it a Major 2nd.
Let's try that with a Major 3rd, and if you play C and E, this is how it works:
Hey dude, I can see you started from C, so that is 1, hmmm, tricky, I can't just count E as number 2, there is a note in between which is D, which is 2 and lastly E, which is 3, are we in the major scale? Yes, I will call it a Major 3rd.
You can see how easy it is.
Note: Whenever you want to build a Major Interval, you should first draw out the notes in the Major scale, and then you start the count from the bottom to the top note.
E.g. If you want to build a D Major interval, the D Major scale is created first, and you build on from there.
Perfect Fourth
Let's take an example of another type of interval:
Going back to our C Maj scale (C, D, E, F, G, A, and B) and let's play (C and F), According to our method, you just played the Fourth interval, C(1), D(2), E(3) and F(4), instead of calling this a Major fourth, we call it a perfect fourth.
Perfect Fifth
The same thing applies to a 5th interval, e.g. (C and G) instead of calling it a Major fifth, you call it a Perfect 5th, no big deal in this naming, it is the name we give different intervals.
Major 6th & Major 7th
Another example is" Playing (C and A) means you played a Major 6th and by playing C and B means you played a Major 7th, it is only 4th and 5th that doesn't have a Major as its name, it's called perfect.
Major 6th interval
Major 7th interval
Note: You can create a perfect 4th and 5th from anywhere in the scale, remember the distance stays the same regardless of the note, (D and G) is a perfect 4th, E and A also a perfect 4th, and so on.
Octave
What if we played the same note, e.g. (C and C), this is called an Octave, they are both the same note, and the interval between the both is 8, more example of an Octave, (D and D), (E and E), and so on.
Distance from the same note is called an octave, it would always be an Octave regardless of where you move
By now, you should probably be able to create a Major, perfect, and Octave interval, let's get to know Minor and Augmented intervals.
Minor Intervals
Minor Interval is easy if you know Major Interval, let's start from somewhere simpler, but before we do, let me make something clear.
You would notice the distance between Major intervals is easy to map out on a Major scale. Things are different on a Minor Scale, knowing a Minor Scale, won't help in getting a Minor Interval.
All you would need to get a Minor Interval is to know the Major interval of a certain distance and then drop the second note by a semitone to get the Minor Interval, let's take an example so you will be able to grasp the idea.
Minor 2nd Interval
We had a major 2nd interval before: C(1) - D(2).
To get the Minor 2nd, you drop the second note (D) by a semitone giving C(1) - Db (b2), since we are dropping it by a semitone, it is advisable to name it b2 (let b(number) stand for minor, e.g. b2, and the whole number stand for major, e.g. (2, 3), b or Flat means to drop lower by a semitone.
You would notice I wrote D♭ instead of C#, if you are moving lower, you use flat, if you are going higher, you use sharp.
Note: Don't worry about the flat or sharp being used, use whatever soothes you, just be aware you can use either depending on the movement.
Play this, and you would notice it sounds different from a Major 2nd.
The distance between a Minor 2nd is a semitone, do you recall that a semitone is two keys together with no key between, so (D - E♭), (E -F) and so on are Minor second.
All you need to remember is a Major second, and dropping the second note by a semitone would give us a Minor second.
Minor 3rd Interval
What about a Minor 3rd?
You guessed the right answer :).
You drop the second note of the Major 3rd by a semitone to get a Minor 3rd, e.g. (C - E) is a Major 3rd, dropping the second note gives us (C - E♭) and that is a Minor 3rd.
Again, Distance always stays the same regardless of where you move.
Augmented 4th
What about a Minor 4th? If you guessed an answer, then I will have to admit you are right, but we don't call it a Minor 4th.
You remember I said we could have a Major fourth, but we call it a Perfect 4th, we also can have a Minor 4th, but we don't call it a Minor 4th, we call it an augmented 4th.
How do you get an augmented 4th?
First, find a perfect 4th, e.g. (C and F), if we try dropping the second note by a semitone, we would have a major 3rd, to get an augmented 4th, we move the second note a semitone higher.
That is we move F to the next semitone (F#), giving us an augmented 4th, why did we choose to name it an augmented 4th, augmented means to increase in number, and in music it means to increase by a semitone.
Minor 6th Interval
Minor 6th: You follow the same method, find Major 6th, drop the semitone of the second note lower to get a Minor 6th, e.g. (C and A), drop the second note by a semitone, by dropping A, we have A♭, then (C and A♭) are called a Minor 6th.
You would notice I wrote A♭ instead of G#, if you are moving lower, you use flat, if you are going higher, you use sharp, view the lesson on Sharp and Flats if you find it confusing.
Note: Don't worry about the flat or sharp being used, use whatever soothes you, be aware you can use either depending on the movement.
Minor 7th Interval
Minor 7th: You follow the same method, find a Major 7th, and drop the semitone of the second note lower to get a Minor 7th.
E.g. C and B, drop the second note by a semitone, by dropping B, we have B♭, then (C and B♭) are called a Minor 7th.
Major 7th interval
Intervals are related to a starting pitch, meaning relations stay the same regardless of where you are on the scale; if it looks overwhelming, you can always come back to this table for reference.
| N of Semitones Apart | Interval | From C |
|---|---|---|
| 1 | Minor 2nd | C - C#/D♭ |
| 2 | Major 2nd | C - D |
| 3 | Minor 3rd | C - D#/E♭ |
| 4 | Major 3rd | C - E |
| 5 | Perfect 4th | C - F |
| 6 | Augmented 4th | C - F#/G♭ |
| 7 | Perfect 5th | C - G |
| 8 | Minor 6th | C - G#/A♭ |
| 9 | Major 6th | C - A |
| 10 | Minor 7th | C - A#/B♭ |
| 11 | Major 7th | C - B |
| 12 | Octave | C - C |
<!-- Music Interval Table -->
We covered the concept of an interval, why they are useful and the naming of an interval in this section, in the next section, we would discuss and see how intervals help in creating Musical Chords in a faster approach, see you in the next phase.
Music Chord
Let's see how to form Chords using interval formulas, not a formula per se, let's call it interval numbers, but before we do, what is a Chord?
A chord is 3 or more notes played simultaneously, that's a pretty cool definition, let's quickly jump into how you can create Major and Minor Chords using intervals numbers.
I mean this is very easy and interesting if you follow the last chapter, please if you haven't viewed the section on Intervals, I will highly recommend you do that, it would open your eyes and brain to how intervals are connected, in terms of relativeness and musicality.
The main practical benefit of learning Chord Theory is that it would open your eyes to the connection between scales and chords, it also helps in connecting the notes that will work out together and help you avoid trial and error.
As I said earlier, a group of 3 or more notes that are played together is called a Chord; let's see how a Chord can be built.
Building a Chord
A Chord can be formed by first selecting the root note of the scale, the root note is the first note of the scale, and we then choose two or more intervals from the scale and build them on the root note to create a Chord.
Let's decipher the meaning by sentence apart:
Firstly, A Chord can be built by selecting the first note of the scale:
Let's say we are in the C Major Scale, (C, D, E, F, G, A, and B), the first note would be C (1), since I am selecting C as my first note, then I will conclude the note C as number 1, that was the reason I wrote 1 beside it, remember "first."
Secondly, we then select two or more intervals from the scale and build them on the root note to create a Chord:
Major Chord
Going back to our C Major scale (C, D, E, F, G, A, and B), let's say you want to build a C major chord.
A major chord contains the root note + major 3rd interval + perfect 5th.
In this case, your root note would be C(1), root note means the first note, selecting the two other intervals in the scale, Major 3rd and Perfect 5th, which gives us E(3) and G(5).
You see how easy it is, all you need to remember for a Major chord is 1 3 5, all you need is the key and by applying (1 - 3 - 5), you would get a Major chord
Altogether, we have the interval numbers (1 - 3 - 5), and that is a Major Chord, you would notice I used the note (C - E - G), the C is the reference note, and it is also the root note, all other notes rely on the root note.
For example, when you see A Major, you'll know the root note is A when you see E, you would know the root note is E, remember root note is number 1, and by adding 3 and 5, means you are creating a Major Chord.
The number 3 is what gives the Chord the name Major Chord since it's a Major 3rd interval, and number 5 is like adding more flesh to the sound.
What about a Minor Chord?
What we created before was a Major Triad, we called it a Triad because it contains three (3) notes, the root, major 3rd, and 5th.
To create a minor triad, all we have to do is substitute the major 3rd for a minor 3rd, giving us the root, minor 3rd, and the 5th.
 To create a minor chord, you substitute the major 3rd with a minor 3rd
To create a minor chord, you substitute the major 3rd with a minor 3rd
The interval number for a minor chord is 1 b3 5.
Do you remember how we figure out the Minor interval, we first get the Major interval and by bringing the second note down a semitone gives us a minor.
If the root position is C(1), to get b3, you flatten the Major 3rd by a semitone, since C is our root note, you flatten E, which gives us Eb (b3), and with the 5th (G), we have a C minor.
The second note is what gives the quality of the Chord, be it a Major or minor.
So, our C minor Triad is C Eb G, another way you can get a minor triad is to select the Root note, the third note in the scale of a minor, and lastly the 5th.
Either way is cool, it all ties down to the building block, which is the interval.
I will suggest you stick with the interval method, with intervals, all you need to remember is the root note, and you can build the rest from there, remember if Major, we use 1 3 5, and if Minor, we use 1 b3 5, the Major Triad is like the foundation of every Chord.
Also, you need to know the key of your song when writing the chord or perhaps the root note of the Chord, if the root were positioned on G, the chord would be G minor, and if on A, it would be A minor or just Gm or Am for short.
Diminished Chord
The diminished triad is a minor triad and a diminished 5th, diminished is the opposite of augmented, diminished means flattening.
For example, in D minor Chord, we have the interval formula of 1 b3 5, which gives us (D - F -A).
To get a D diminished, you flatten the 5th, giving us the (D - F - Ab), interval formula would be (1 b3 b5), the root note (1) is on D, so we call it D diminished or D dim for short.
To get a diminished chord, flatten the third and 5th in Major scale, or flatten the 5th in a minor chord
- Note: Don't worry about the flat or sharp being used, use whatever soothes you, just be aware you can use either depending on the movement.
More example, C minor Chord is (C D# G), to get a C diminished, you flatten the 5th, giving us the (C Eb Gb), interval formula would be 1 b3 b5, the root note (1) is in C, so we call it C diminished, or C dim for short.
Also, Diminished is known as a minor flattened, it is a minor triad with the 5th flat or dropped by a semitone, and that's all you need to know about Diminished Triad, is it that easy? Yes, as you can see yourself.
One last thing, Diminished is shortened with a degree sign next to the root note, e.g. C° or F°, who cares about signs, I want you to know they can be shortened as well.
Major Key Relationship
I would show you the essential aspect you need to know before writing a good chord progression in this chapter.
Before you start writing chord progression, you need to know the relationship between a Chord and a Scale.
Most people learn about Chords and Scale, but very few learn about the significant relationship between them, it is so easy that some people aren't aware of the simple underlying relationship between the two.
Once you know the relationship between both Chords and Scales, which I am about to show you, it would help you in approaching Chords in a much faster way, and it will instantly increase the way you write Chord progression, let's dive in.
The relationship between a Chord and a Scale is that a Chord is built on each degree of a Scale.
For example, the major scale has 7 degrees (degree means a position on a scale, C is a position, D is a position, you get the idea!) and we can, therefore, build seven (7) chords in a Major Scale.
C Maj Scale is made up of (C, D, E, F, G, A, and B) (7 degrees), which means we could create seven (7) chords from each degree by rooting every note on each degree.
(C Maj, D min, E min, F Maj, G Maj, A min and B dim) are the Chords in the C Maj Scale (would tell you the reason we have a minor chord and diminished chord, later on, keep reading!).
If you play [C Maj, F Maj, and G Maj], you would know the Progression is compatible with a C Major scale and if you play [C Maj, D min, and G Maj] you would also know it is compatible with the C Major Scale because the Chords occur in the C Major Scale.
I think you got the idea, but that is not where I am leading you, it doesn't make sense for you to perceive the arrangement of Chord this way, although, it works, that perception would take longer than ever.
What if we think of the Chord Scale system in numbers, that is the numbers would work for any given Major Scale (C Maj scale, D Maj Scale, and the likes) as long as you follow the relationship.
All we do is build Chords on each degree of the Major Scale and assign it a Roman numeral according to its quality, if you do think this way, you would be able to build the same relationship over other notes, and everything would stay the same.
No more cramming if one notes are compatible with another note in a given key
This is how it works:
You start by building a triad on each degree of the Scale, I am glad you now know intervals works, so this should be very easy, all you need to remember for now is the number 1 3 5, and that's all about a Triad, forget about 1 b3 5(Minor) or 1 b3 b5(Diminished) for now, just remember 1 3 5.
! you forgot how intervals work, please take a refresher from the interval chapter!
Let's build Chords on the 7 degrees(remember degree means a position on a scale!) in CMaj Scale,
(C, D, E, F, G, A, and B)
We build a chord from their root note, and the degrees note becomes the root note.
Since we are starting from C, C is the root note, which is 1, E is number 3 and G is number 5, which gives us C Major ( C - E - G).
C is the first degree of the scale, we then build the rest on it, all you need to remember is 1 3 5
The number 1 3 5 would determine if we would call it a Major, Minor or diminished, as for the first one, it is a Major and let us represent it with an upper case Roman numeral I.
1. I
Let's move on to the second degree, which is D, now D becomes the boss, the root note is D, and using the number (1 - 3 - 5), we get a D minor (D - F - A).
Let's represent this one with a lowercase Roman numeral ii (since it is minor, it makes sense to represent it with a lowercase).
2. ii
Note- I used Roman numerals ii since it is in the second degree
Why is the second degree a minor chord and not a Major chord as we are in the Major scale, the answer is simple.
It is because the interval of the scale dictates if a minor third(b3) is used or a Major chord is used (3), that is the reason why I said you should forget about the b, and only think of the number (1 - 3 - 5).
The number (1 - 3 - 5) would determine if you are to use a Major or a Minor as we are strictly restricted to using the notes in the scale (sometimes it is not always the case when writing progression but assume it is for now).
Note: You only count the numbers in the given scale and not outside of the scale, if you do things this way, you would always be correct with the given Chord, let's progress.
Moving on to the third degree which is E, E now becomes the boss, the root note of the third degree, and by using the interval numbers (1 - 3 - 5), we get an E minor (E - G - B), again we represent it with a lower case roman numeral iii.
3. iii............Skipping the 4th degree, 5th degree and 6th degree, which would give you
4. IV
5. V
6. vi
Note: Major is represented with a Capital case roman numeral, and a Minor is represented with lower case Roman numerals, and how did I know which to represent with Major or Minor, I used the interval number (1 3 5).
I intentionally jumped those numbers since they represent Major or Minor and you can use the above method to figure out the Chord.
The last degree in C Maj Scale is B which is the 7th degree of the scale and also the last note in CMaj Scale, now B becomes the boss, and it becomes the root note, and by using the interval numbers (1 - 3 - 5), we get a B diminished chord.
It is a diminish because the interval number (1 - 3 - 5) dictated a diminish Chord in the 7th degree, you remember I said you should focus on the interval numbers (1 - 3 - 5) for now and you learned in the Diminish Triad lesson that a diminished chord is represented with a degree next to it and that gives us vii°.
7. vii°
Altogether we have:
1.(I)
2.(ii)
3.(iii)
4.(IV)
5.(V)
6.(vi)
7. (vii°) - 7 chords on each degree!
The capital roman numeral indicates a Major, the lower indicates a minor, and a lower roman numeral with a degree sign indicates a diminished Chord.
This is where things would get interesting:
If you are told to play (I - IV - V), you would know (I - IV - V) is referring to the 1st, 4th, and 5th chords of the scale.
And if (I - ii - iii), you would know it is referring to the 1st, 2nd, and 3rd of the scale without even cramming the notes of the scale, you can see how this help in understanding the relationship of the chords without specifying the key.
The magic of knowing this relationship is that it works for every Major scale; the relationship between the Chords is the same, just like the scale intervals.
If a composition is in D major, then it means we are in the tonal center of the composition and this determines the chord structure.
In layman's terms, D would hold position number 1 since we said we are composing in a D Major Scale.
It means the tonic chord is D, and then you build up from there, the next note is E, and it represents a minor chord, and so on.
Tonic means the keynote or the first note or the first degree of the scale.
What I am pointing out is that the roman numeral.
1.(I) 2.(ii) 3.(iii) 4.(IV) 5.(V) 6.(vi) 7.(vii°)
Would also work for the D major (in fact any major scale), you can see it makes a lot more sense to think in the relationship.
You can see the same relationship works for D major scale, that's the power of knowing the relationship, all you need to know is the key of the song, and by applying the relationship, it would always stay the same
All you need to remember is the key to a song.
If a song is composed in G Maj, then you know G is number 1, and by following up the order of the Roman numeral, it would always be the same no matter the key you are in.
If it is composed in C Maj, you know C is number 1 and by also following the order, they will always be the same, and so on.
The Chord Scale relationship is not limited to writing Chord progressions, although, millions of good songs have been using this same basic idea, which we will be expanding on in upcoming lessons.
I am glad I pointed out the relationship between Scale and Chords, in the next lesson, we would explore how this relationship helps in writing a good Chord progression.
Basic Chord Progression
If you got to this point, then I will have to congratulate you for following up on this course, by now you should firmly grasp the idea and understanding of sharps and flats, Semitone and Whole Tone, Scale, Intervals, Basic Chords, and the Relationship between Chord and Scale.
We aren't putting anything into practice in previous chapters, and it is just like learning the alphabet, you start by calling letters one after the order, and then you gradually progress into calling out words.
I did the same thing in this guide, I started from the basics, and we gradually progress.
Now, I would show you how to form and write a meaningful Chord progression using the basic Chord you learned in previous lessons, sit back, relax and focus on how to do it the right way.
The Key of Your Chord Progression
The concept of keys in music is important as other elements of composing a piece of music are essential, the idea is sometimes confusing, but let me get it straight into your head with a cool analogy.
Some say:
Key is the musical center of gravity that all other object is constantly pulled toward it until it comes to a state of rest on their surface.
Even if this explanation looks simple, a number of questions might arise, like "What is the Center of gravity, and how does that relate to the Key?"
Analogically, I won't take this route in explaining the concept, let's take another route.
A key is a table of content around which a piece of music(content) revolves, if you think of it in this direction, then you will grasp the idea.
Think of a Key like a book, which contains a Table of content (table of content is the scale, e.g. Major or minor), when a song is played in a particular key, the song revolves around the notes in the key, that is you select the notes in that specific key to play the song.
So, firstly, you choose the key of your song (the book), if the key is C Major then you use the notes in C Major (the table of content) (C, D, E, F, G, A, and B), the notes make up the melody, bassline, chord and the song in whole.
The Tonic of The Key
The root note of the key is the first note of the scale or the first degree of the scale.
The tonic note or root note is the fundamental note in the scale, and all other notes are based on the root note.
Think of the tonic as the first chapter in the book, whenever you are reading a book, you will always want to start from the first chapter and move on from there.
It is the same with the tonic note, and you will always want to begin on the tonic and land on the tonic sometimes.
Another way to think of a Key is a Tap of a liquid substance, but in this case, the liquid is the notes of a given scale (let liquid denote notes).
When you switch on the tap, the first notes that will flow out is the root note or Tonic, while other notes will flow after the tonic and when we switch off the tap, all other notes will eventually want to pull back to the tonic. You got the idea, right?
I guess I tried simplifying things, so let's start with writing a basic Chord progression.
What I am about to show you is how to use the relationship you learned in the last lesson to write a meaningful chord progression.
A chord progression is simply the series or the sequence of chords. Whenever you listen to music, you would often hear chord changes, and this is what gives you the feeling of being taken on a journey.
Do you remember the Tap analogy, the tonic is the first note that flows out of the tap, and the other chords can be seen as a journey away from the tonic or the home
Eventually, the notes would want to pull back to the tonic note, remember when you switch off the tap.
The 1- 4 - 5 in Major
Certain movements work between the Tonic chord and other chords in the relationship that naturally works, that is the reason I covered the relationship in the last lesson, from this table let's pick the I - IV - V relationship.
The Major Scale Relation Table:
| Degrees | Roman | Chord |
|---|---|---|
| 1 | I | Maj |
| 2 | ii | min |
| 3 | iii | min |
| 4 | IV | Maj |
| 5 | V | Maj |
| 6 | iv | min |
| 7 | vii° | dim |
<!-- Major Scale Rel Table -->
I am picking this because it has been used in music for centuries and it has been the simple chord formula for lots of hit songs right out there.
I'll be writing the chord progression in the key of E Maj, and this is my final result:
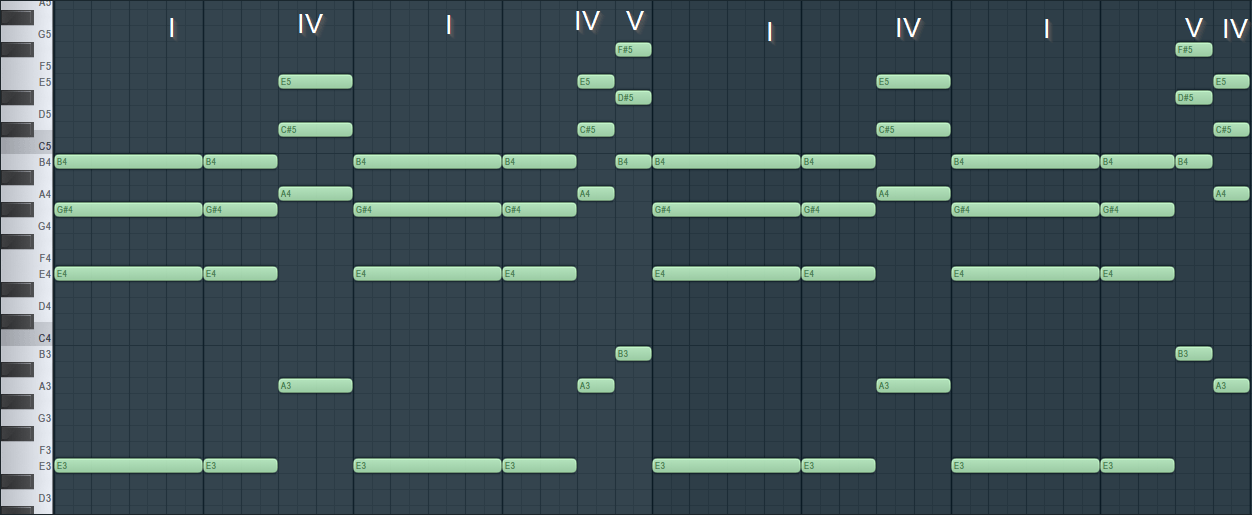
I ended up having [(I - IV - I - IV - V) / (I - IV - I - V - IV)]
Confusing?
It shouldn't be, all I was doing was reshuffling the chord, you don't have to play it in the order (1 4 5), mix things around and try to be creative, I am already thinking of hundreds of ways to create a different progression using those three natural relations.
That's the power of the relationship, whenever I am stuck, I always refer to this and I would still come out with writing a meaningful good chord progression.
It shouldn't always be the (1 4 5), they are other natural chord sequences you can pull from the diatonic scale (Diatonic means in key or notes in the scale).
My best advice for you now is to follow up the guide carefully, and by the end of taking other chapters in this guide, you would be able to create a good chord progression.
In the next chapter, you would learn how to use inversion to enhance your chord progression.
Chord Inversion
In our last chapter, we covered how to write a meaningful chord progression using the relationship between Chord and Scale, in this lesson, you will learn how to create a more advanced Chord progression by learning to invert your chords correctly.
We would be building on the Chord progression we used in the last chapter, and in upcoming chapters, we would be writing different types of Chord progression using the so-called relationship.
Now, let's look at how to make the chord progression we created in the last lesson even more interesting.
Our goal is to focus on using inversions to make our chord interesting!
Note: Inversion is easy, and all I would have to tell you about inversion is to focus on what you hear, that is, focus on what sounds best to you.
What is Chord Inversion
A chord inversion is where the root note is not the lowest note, that is, it has been moved away from the root note, although it remains the same chord but just a different ordering, and that's it. Simple!
I would show you how to create an inverted chord in a moment!
Advantages of Using Inversion
The main benefit of using Chord inversion is to make the quality of the chord better, the harmony would flow seamlessly with one another, and it doesn't change the character of the note (just re-ordering).
Another reason why you should use inversion is when you want to move with ease, using your fingers (this is if you are a pianist).
Problem:
The root note is always at the bottom, and when you play, you would still need to shift your fingers around the keyboard causing longer and unnecessary movement, although you would become perfect with enough practice.
Solution:
To avoid this, you rearrange the order of notes for the specific chord to help in the process of moving near to other root notes, without longer stretching, and also help in the process of smooth transitions between two notes.
As for me, I create my composition directly in the Daw, and the only reason I use inversion is to smooth things up, this depends if it sounds good to me, and if it doesn't, I would mostly leave the composition as is.
Now that you have known the advantage of using a Chord inversion, let's see how to create and use an inversion.
There are two possible inversions in a Triad, the First(1st) inversion, and the Second(2nd) inversion.
The First Inversion
Let's learn how the first inversion works in the C Major Triad, and we would use this in enhancing our previous chord progression.
The C Major Triad is 1 3 5 consisting of C (The Root or 1), E (the 3rd), and G (the 5th). C is in its root position, so there is no inversion here, simply C E G.
C is in its root position, so there is no inversion here, simply C E G.
If you reorder the note and place E on the bottom, it means the C major chord is in the first inversion, giving us 3 5 1, E G C.
If you reorder the note and place E on the bottom, it means the C major chord is in the first inversion, giving us (3 5 1) or (E G C).
Do not confuse root note and bass, the root note is the note on which the chord is built, while the bass is the bottom note or, the lowest note of the chord.
The first inversion of C Major is (E G C), E has been reordered to the bottom, and the root note has been re-order to the top, giving us the first inversion. In the first inversion, the third is the lowest note.
The Second Inversion
What if we reorder the note and place G on the bottom, this would give us a Second inversion, (5 1 3) or (G C E).
In the second inversion, the 5th is the lowest
Again, do not confuse the root note and bass, the root note is the note on which the chord is built, in this case, it's a C. While the bass is the bottom note of the Chord.
In the second inversion, the fifth is the lowest note.
Summarising Inversion in Triad:
Whenever you have a Triad, or 3 notes Chord, in the first inversion, the 3rd interval would be the lowest note, and in the second inversion, the 5th would be the lowest note.
Now, let's build and enhance our previous Chord progression.
Again, when using inversion, focus on what sounds best to you and not what you see.
Note: N-I means no inversion, F-I means the first inversion and S-I means the second inversion
You can see how the chords connect seamlessly together, that's the power of using inversion, you don't have to use inversion.
I use it whenever I feel like it, and when I believe my chord progression needs closeness, I mostly experiment with inversion.
You can see the difference between learning music theory and pressing random notes.
When you know the theory behind a composition, you know what works and what won't work. Sometimes, things are different; in that case, you leave it as is if it's good.
It's your turn to use inversion!
Minor Key Relationship
Up until now, we have been discussing and experimenting with the Major key chord relationship, that is we have been using Major Scale to build chords on each degree of the scale.
In this lesson, you would learn how to use a Minor scale to build a minor key relationship, which requires a new Tonic center.
This concept is the same as the one you learned in the previous lesson, in the last lesson you built a chord on each degree of a Major scale, while in this lesson, you will build a chord on each degree of a minor scale.
The minor scale has 7 degrees, and we can, therefore, build seven (7) chords in a minor scale.
For example, C minor scale is made up of C, D, E♭, F, G, A♭, and B♭, which means we could create seven (7) chords from each degree by rooting every note on each degree of the scale.
Again, to get the minor chord relation, you start by building a triad on each degree of the scale, and, all you need to remember to do this is the number 1 3 5 (as we did in the Major key relationship).
The interval number 1 3 5, would determine if we call it a minor, Major, or and diminished chord.
Note: You are restricted to counting the notes in the scale
I won't start by showing you how to build the chord on each degree of the minor scale; we already did that in the Major Key Relationship, I got an illustration for you:
There are seven chords on each degree of the minor scale
If you properly build the chord on each degree of the minor scale, you should get something like this:
The Minor Scale Relation Table:
| Degrees | Roman | Chord |
|---|---|---|
| 1 | i | min |
| 2 | ii° | dim |
| 3 | III | Maj |
| 4 | iv | min |
| 5 | v | min |
| 6 | IV | Maj |
| 7 | VII | Maj |
1.(i) 2.(ii°) 3.(III) 4.(iv) 5.(v) 6.(VI) 7.(VII)
You can see these relations are different in the minor scale; in this case, the tonic is a minor chord while in the Major scale, the tonic is a Major chord. (The tonic is the first note of the scale or the home key)
If you carefully look at the minor scale relations, you would see it is the same with Major scale relations, all we did here is reposition the scale in relation to the 6 (vi) becoming 1(i) in a minor scale, 7(vii°) becoming (ii°) in a minor scale, and the interval of the scale continues from that point.
The Below Table Give a Better View:
| Degrees | Roman | Chord |
|---|---|---|
| 6 (vi) | 1 (i) | min |
| 7 (vii°) | 2 (ii°) | dim |
| 1 | 3 (III) | Maj |
| 2 | 4 (iv) | min |
| 3 | 5 (iv) | min |
| 4 | 6 (VI) | Maj |
| 5 | 7 (VII) | Maj |
The tonic of the minor chord is what allows us to create a song "in the key of _minor."
and the tonic of the Major chord is what allows us to create a song "in the key of _Major", pretty explanatory.
I hope you got the concept of the Minor key progression, and we would use this relation to create Chord progressions in the next lesson.
Chord Progression In a Minor Key
In the last part, we looked at some natural relationship that helps define a Major key Chord progression, that is we have been building some interesting progressions in the Major scale, using relations.
In this lesson, we would build a minor key chord progression using the same relationship that occurs in the minor scale, let's get started.
The 1- 4 - 5 in minor
The minor Key Table:
| Degrees | Roman | Chord |
|---|---|---|
| 1 | i | min |
| 2 | ii° | dim |
| 3 | III | Maj |
| 4 | iv | min |
| 5 | v | min |
| 6 | IV | Maj |
| 7 | VII | Maj |
We used the 1 4 5 (I - IV - V) relationship in the Major key chord progression, let's use the same for our minor key chord progression, remember we are starting from the minor tonic, and the roman numeral will be( i ) as opposed to the Major ( I ).
Basically, this is the roman numerals in the minor scale: 1. (i) 2. (ii) 3. (III) 4. (iv) 5 .(v) 6. (VI) 7. (VII)
1 4 5 movements in the minor would be i - iv - v in the table above, it is easy, when someone tells you to play 1 4 5 in key G minor, you know you would be working with the minor scale relation and when you play in the key of G or G Major, you would be working with the Major scale relation.
Again, our goal is to mix things up, and it doesn't have to be in the order, I ended up having [ (1 5 4) / (1 4 5 4) ] or [ (i - v - iv) / (i - iv - v -iv) ]
The 1- 5 - 4 - 6 in minor
There are lots of other movements you can experiment with within the minor scale. In this section, I'll use the (1 - 5 -4 - 6) in minor key progression.
The minor Key Table:
| Degrees | Roman | Chord |
|---|---|---|
| 1 | i | min |
| 2 | ii° | dim |
| 3 | III | Maj |
| 4 | iv | min |
| 5 | v | min |
| 6 | IV | Maj |
| 7 | VII | Maj |
If you carefully look at the minor table above, you would notice that (1 5 & 4) is a minor and the 6th is a Major, I call this mixing the "the chord quality movement."
The chord quality movement makes your progression interesting, it makes it feel natural, and to be sincere, 90% of my chord progressions use this mixture.
In the previous chapter, I told you to mix the order of the movement, although, you don't have to do that, just want you to know, when you reshuffle the order around, there are thousands of possible combinations you would come across.
Most time, it makes sense to your chord progression simple, I won't mix the order, I will leave the order as is, (1 5 4 6) or (i - iv - v - VI).
This progression has no inversion
There is nothing wrong with this progression, but we can enhance it by using inversion, you remember inversion helps to smooth things up, and it makes your chord looks stable and interesting.
Note: N-I means no inversion, F-I means the first inversion and S-I means the second inversion
Progression 1 5 4 6 inverted
It seems everything is getting interesting, I will further make the chord progression even more interesting by chopping up the chords, and this is what it looks like:
Progression 1 5 4 6 chop inverted
You don't have to do it this way, feel free to experiment
Feel free to use other combinations from the relationship, test things out and select your favorite movement.
Melody Secret You Never Knew
In this lesson, I will build a melody on the chord progression we created in the last lesson.
Melody creation should be another course entirely and doesn't quite fit this section. Even with that said, I'll teach you a trick I use for melody creation when I am stuck, it works most of the time.
The Moving Note Method
I am gonna show you kind of like a melody trick I have been using for some time. I call it the moving note method, and this is what it means:
1.) The first step is to listen to the chord progression more than twice, and then I sing along the root note of each chord in the progression or perhaps hum the chord progression.
You would notice as you sing along the chord progression, you are landing on the root note of each chord.
This is what it sounds like:
<!-- humming the chord progression -->
In this case, you use your mouth to hum, when you hum the root note of each chord in the progression, it helps your brain in registering compatible notes that are likely to work out for your melody line.
2.) The next step is to escape from humming only the chord root note, try pushing yourself to other notes (try to be creative here) as you hum along with the chord progression, it forces you to pick out notes that are likely to work or compatible notes for your melody.
This is what it sounds like:
<!-- Escaping From The Degree Note -->
Note: Don't hum in your mind, hum out and listen to yourself!
3.) When you are done with this stage, try to draw out the melody you have in your head before it tears off, proceed if it's cool, you should proceed and if not, go back to stage one until you are satisfied with a better melody.
And the final result:
<!-- and the final result -->
See how easy it looks, if it is not working for you, relax and try again, it is not something you can learn in a few minutes, you have to keep trying until you master the art.
It shouldn't take long!
Request If You Want Me To Create a Full Song Out of This
It's Your Turn To Shine
I hope you enjoyed my guide to learning the basics of music theory.
I would like to hear from you:
Which part or section do you find the most interesting?
Let me know by leaving a quick comment below.